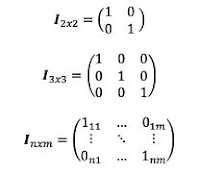lunes, 24 de mayo de 2021
Matrices Especiales
Las matrices que a continuación enumeramos, son matrices que generalmente se encuentran en los diferentes problemas y trabajos en algebra lineal.
Matrices especiales (Todas las matrices son cuadradas).
Matriz identidad.
Propiedades de la matriz identidad
Matriz diagonal.
Es una matriz en la cual los elementos que no hace parte de la diagonal, es decir que su índice de fila y columna son diferentes entonces son cero.
Matriz triangular superior.
Como vemos en la imagen, si los elementos que se encuentran por debajo de la diagonal principal son cero entonces tenemos una matriz triangula superior.
Matriz triangular inferior.
Si los elementos por encima de la diagonal principal son cero entonces tenemos una matriz triangular inferior.
Matriz Transpuesta.
Si en una matriz intercambiamos las filas por las columnas estaremos transponiendo la matriz.
Matriz Simétrica.
Se obtiene una matriz simétrica cuando obtenemos una matriz igual al transponerla.
Matriz Antisimétrica.
Una matriz antisimétrica se obtiene cuando la matriz transpuesta es igual y tiene signo contrario.
Matriz Aumentada.
La matriz aumentada es la representación del sistema de ecuaciones aumentado con el vector de resultados.
Matriz Ampliada.
La matriz ampliada es la unión de la matriz de nuestro sistema y la matriz identidad. Esta matriz la podemos usar con el método de Gauss-Jordan para encontrar la inversa también.
Ejemplo.
sábado, 8 de mayo de 2021
Aplicación del álgebra matricial para la solución de sistemas de ecuaciones lineales
Aplicación del álgebra matricial para la solución de sistemas de ecuaciones lineales
Solucion de sistemas de ecuaciones lineales usando matrices
resumen sobre los diferentes métodos que se aplican para solucionar sistemas de ecuaciones utilizando las matrices
Definiciones:
Una matriz de orden mxn es un arreglo rectangular de mn elementos dispuestos en m filas y n columnas.
Matriz transpuesta es la matriz que se le intercambian las filas for las columnas siendo T(aij) = bij = aji
Matriz simétrica es la matriz que su transpuesta es igual a la original, y antisimétrica es la matriz que su transpuesta es igual a la original con signo negativo.
Las matrices diagonales y triangulares juegan un papel importante en la descomposición de matrices que sustentan los algoritmos mas importantes del algebra lineal.
La diagonal principal de la matriz está conformada por aquellas entradas donde los subíndices son iguales i =j.
(i) Filas (j) Columnas
Una matriz es diagonal si y solo si todas las entradas de la diagonal son diferentes de cero y el resto son ceros.
Una matriz es triangular superior si y solo si todas las entradas donde los subíndices son i>j son cero.
Una matriz es triangular inferior si y solo si todas las entradas donde los subíndices son i<j son cero.
Un sistema de m ecuaciones lineales con n incognitas AX = b es soluble si existe al menos un vector S de n componentes constantes tal que AS = b. A un sistema que carece de solución lo llamamos no soluble o inconsistente.
Hay operaciones elementales de fila.
1. Sustraer a una fila un múltiplo de otra
2. Intercambiar dos filas
3. Multiplicar una fila por una constante diferente de cero
Método de Gauss-Jordan
Es un algoritmo para eterminar simultaneamente si una matriz cuadrada A tiene inversa y también resolver el sistema de ecuaciones.
Determinante
El determinante es una propiedad de las matrices que se obtiene realizando diferentes algoritmos. Esta propiedad contiene información obre la matriz y la solubilidad del sistema de ecuaciones
Regla de Cramer.
Es un método que usa determinantes para hallar la solución al sistema de ecuaciones.
Responder a las siguientes preguntas:
a. ¿Cual de los métodos es el más indicado para resolver un sistema de cuatro ecuaciones con cuatro incógnitas y por qué?
sin lugar a dudas el método de Gauss-Jordan es más eficiente computacionalmente.
b. ¿Que ventaja tiene resolver un sistema de ecuaciones dos por dos con el método de determinantes?
Los métodos con determinante para solucionar sistemas de ecuaciones previenen de realizar cálculos en exceso ya que el determinante del sistema no puede ser cero. ya que para usar la regla de Crammer la matriz debe necesariamente ser invertible.
c. Enumere al menos tres métodos para calcular un determinante.
Método de cofactores: consiste en escoger una fila o una columna, para cada término de la fila o columna, llamados cofactores, quitamos la fila o columna en la que está y lo que queda es el menor.
Después, multiplicar el valor del menor por el cofactor y por su signo y sumar lo de todos los cofactores
El determinante de una matriz de orden n se puede calcular de n^2 maneras diferentes ya que el desarrollo por cofactores se puede realizar por filas o por columnas.
Método de Sarrus: también llamado la estrella de David consiste en 2 partes, la primera es sumar la multiplicación de la diagonal, más la multiplicación del primer triángulo formado a la derecha de este y su inverso, a esto se le resta la multiplicación de la diagonal secundaria más el triángulo formado a su derecha más su inverso
Método único para matrices de 3x3: Este método consiste en aumentar a la derecha las dos primeras columnas o abajo las dos primeras filas de tal manera que con estas obtengamos la multiplicación de las diagonales principales y sumar sus productos de cada una y restar de este valor la suma de las multiplicaciones de las otras diagonales.
Solución sistema ecuaciones método de Gauss-Jordan
Método de Gauss – Jordan
El método de Gauss – Jordan consiste en transformar la matriz aumentada del sistema en una matriz diagonal usando únicamente operaciones elementales, proceso relativamente simple, ya que podemos elegir arbitrariamente la operación elemental más conveniente, así como los escalares más adecuados que se utilizarán como factores. Así el sistema:
Tiene matriz aumentada
La cual podemos llevar a una forma escalonada por medio de operaciones elementales de fila
Existen tres operaciones y estas son:
Operaciones elementales en Filas:
i) Multiplicar (o dividir) una Fila por un número diferente de cero.
ii) Sumar un múltiplo de una Fila a otro renglón.
iii) Intercambiar dos Filas.
El proceso de aplicar las operaciones elementales por renglones para simplificar una matriz aumentada se llama reducción por renglones.
Notación:
1. Ri → cRi quiere decir “reemplaza la i-ésima Fila por esa misma Fila multiplicado por c”. [Para multiplicar la i-ésima Fila por c se multiplica cada número en la i-ésima Fila por c.]
2. Rj → Rj + cRi significa sustituye el j-ésima Fila por la suma de la Fila j más la Fila i multiplicado por c.
3. Ri ⇄ Rj quiere decir “intercambiar las Filas i y j”.
4. A → B indica que las matrices aumentadas A y B son equivalentes; es decir, que los sistemas que representan tienen la misma solución.
La matriz aumentada llevada a una forma diagonal mediante operaciones elementales, se tiene:
La cual equivale al sistema:
Que tiene solución:
La diferencia entre este método y el método de Gauss es que este método lo estamos aplicando directamente a una matriz a diferencia de aplicarlo al sistema de ecuaciones y obtenemos una sistema escalonado. El método de Gauss-Jordan finaliza cuando encontramos la matriz escalonada reducida.
El beneficio de realizar el método de Gauss Jordan es que para una matriz de un grado muy grande nos permite realizar los cómputos de una manera simple y aunque puede ser largo solo usaremos tres operaciones elementales.
lunes, 22 de marzo de 2021
Presentación Auditoría de sistemas
En este apartado alojaré las actividades desarrolladas en la materia de Auditoría de sistemas.
viernes, 19 de marzo de 2021
Presentacion Algebra Lineal
En este apartado están anexos los trabajos y evidencias del curso de Algebra Lineal G100 IUPB.
Suscribirse a:
Entradas (Atom)