Las matrices que a continuación enumeramos, son matrices que generalmente se encuentran en los diferentes problemas y trabajos en algebra lineal.
Matrices especiales (Todas las matrices son cuadradas).
Matriz identidad.Propiedades de la matriz identidad
Matriz diagonal.
Es una matriz en la cual los elementos que no hace parte de la diagonal, es decir que su índice de fila y columna son diferentes entonces son cero.
Matriz triangular superior.
Como vemos en la imagen, si los elementos que se encuentran por debajo de la diagonal principal son cero entonces tenemos una matriz triangula superior.
Matriz triangular inferior.
Si los elementos por encima de la diagonal principal son cero entonces tenemos una matriz triangular inferior.
Matriz Transpuesta.
Si en una matriz intercambiamos las filas por las columnas estaremos transponiendo la matriz.
Matriz Simétrica.
Se obtiene una matriz simétrica cuando obtenemos una matriz igual al transponerla.
Matriz Antisimétrica.
Una matriz antisimétrica se obtiene cuando la matriz transpuesta es igual y tiene signo contrario.
Matriz Aumentada.
La matriz aumentada es la representación del sistema de ecuaciones aumentado con el vector de resultados.
Matriz Ampliada.
La matriz ampliada es la unión de la matriz de nuestro sistema y la matriz identidad. Esta matriz la podemos usar con el método de Gauss-Jordan para encontrar la inversa también.
Ejemplo.

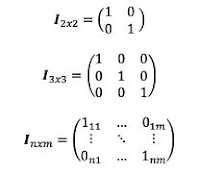









No hay comentarios.:
Publicar un comentario